Ben Lansdell

Ben Lansdell

Machine Learning Engineer & Applied Mathematician

Ongoing projects

Ongoing projects

Functional connectivity in concurrent-use BCIs

Functional connectivity between populations of co-tuned (similar color) and BCI-control units (square units)

Brain-computer interfaces (BCIs) provide insight into the cognitive processes underlying sensorimotor control. While the relevant neural populations involved in control and learning of a new motor task are in general difficult to identify, with a BCI the neurons most directly responsible are known exactly, by construction. This allows the control and learning process to be observed more directly, which in turn is beneficial to understanding the neural adaptations that are required for neuroprosthetic control. Previous research shows that proficient control involves the establishment of stable neural ensembles associated with the BCI. However, the design of robust and flexible BCIs that can be operated in conjunction with ongoing behavior requires an understanding of how this circuitry established for brain-control interacts with existing, potentially competing, neural circuits. In conjunction with Prof. Chet Moritz, Adrienne Fairhall and Ivana Milovanovic, through a dual-control BCI in a non-human primate, we study how motor cortex accommodates BCI control alongside concurrent wrist motion.

Neuron and behavior tracking in a model cnidarian

Kalman filter for tracking Hydra pose through video in order to aid neuron tracking

Large scale recordings of neural activity in freely behaving animals promises to uncover much about the relationship between neural activity and behaviour. Particularly exciting is the possibility of recording intracellular calcium of whole organisms in conjunction with unconstrained behaviour. Tracking neurons throughout such recordings poses a significant image processing problem. Current approaches in both planar and volumetric imaging rely on semi-automatic, curated tracking algorithms, which must be manually checked for consistency. In collaboration with the Yuste lab at Columbia University we are working on methods to improve automated neuron tracking. Using a high-dimensional state-space model to track a parameterized mesh of the Hydra at each frame allows for more robust neuron tracking. The method is implemented with GPUs to improve performance. In the future we hope to explore more realistic, biomechanical models of the Hyrda.

Previous projects

Cholinergic retinal waves as traveling pulses in an excitable medium

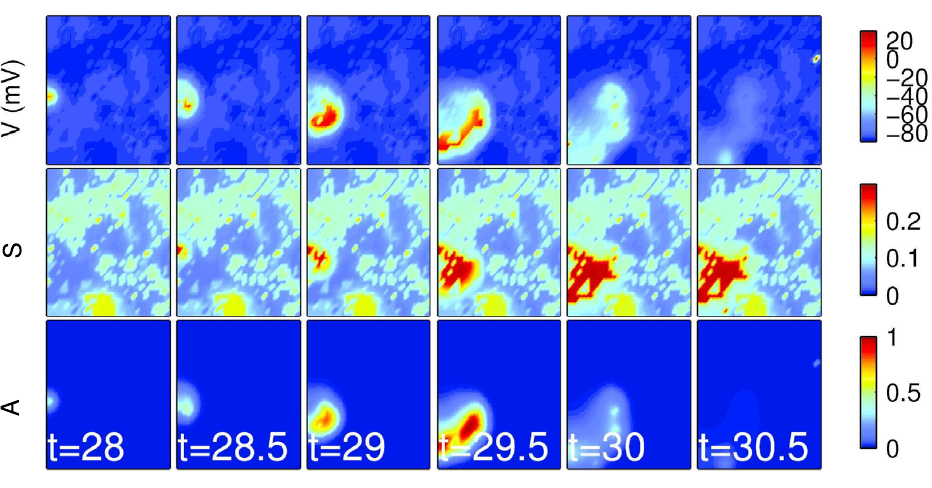
Frames from simulation of retinal waves model. Top frames show a spreading wave of depolarizing amacrine cells modulated by a slow refractory field (middle frames) and an extra-cellular acetylcholine concentration (bottom frames).

In collaboration with Prof. Nathan Kutz and Dr. Kevin Ford, we developed a reaction-diffusion model of correlated spontaneous activity in the developing retina — activity known as retinal waves. Here, the developing retina was modeled as an excitable medium, allowing for the existence of retinal waves to be predicted above an excitability threshold that is determined from the model’s analysis. The approach is novel in its ability to determine such a criterion in a semi-analytic fashion. This was achieved by separating the dynamics into fast and slow timescales and using numerical continuation software to determine the existence of a traveling wave front for some combinations of the model’s parameters. Above you’ll find a numerical simulation of the model.

On bistability as a control mechanism of intrinsic apoptosis

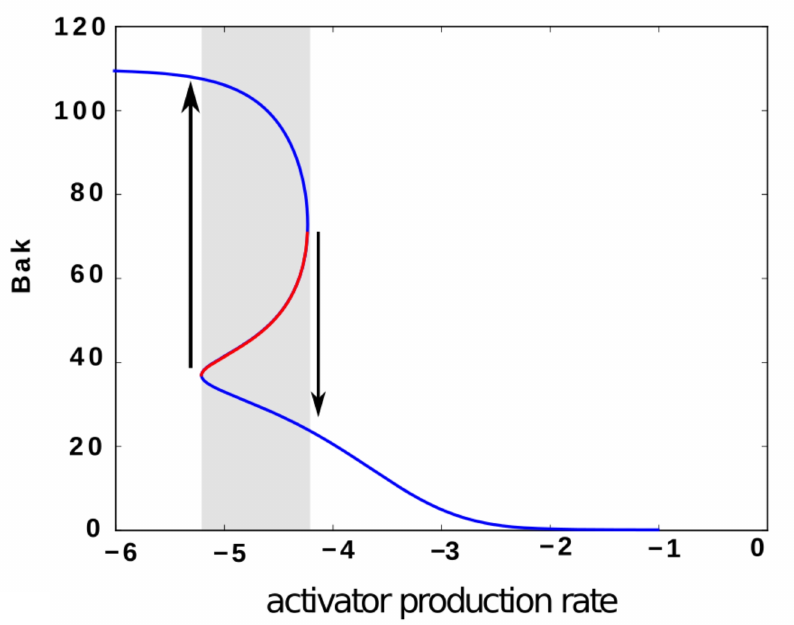
Proposed control mechanism of Bcl-2 regulated apoptosis is through bistable dynamics shown here. Inert Bak is (in)activated in a discontinuous fashion, providing a robust switch.

Intrinsic apoptosis (programmed cell death) is regulated by the Bcl-2 family of proteins, whose interactions on the mitochondrial membrane, on receiving sufficiently strong pro-apoptotic signals, can initiate caspase activation — a point of no return for the cell. Determining how this regulation is implemented, and how it can malfunction, is important for the development of anti-cancer therapies. With Prof.s Terry Speed, Kerry Landman and Ruth Kluck, we developed a kinetic mass-action model of Bcl-2 interactions relevant to a simplified mitochondrial assay containing only a subset of Bcl-2 members. A proposed theoretical control mechanism through which the Bcl-2 family may regulate apoptosis is a bistable switch. By careful calibration of our model with known and estimated kinetic reaction rates we show that bistability is unlikely to play a role in the reduced assay.

Integrating genomic tiling array data into gene prediction with generalized hidden Markov models

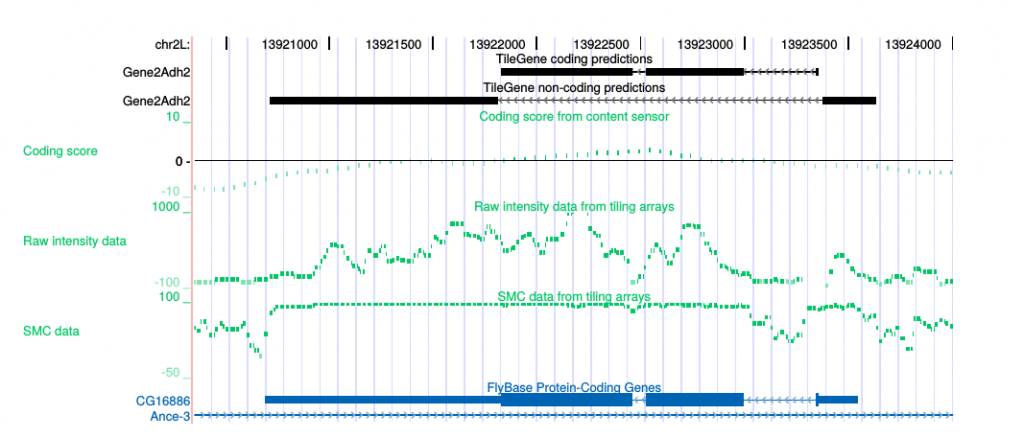
Incorporating mRNA expression data (center) with genomic DNA signals to predict coding and non-coding eukaryotic gene structures (top).

My honours project, with Tony Papenfuss, was in computational gene prediction, in which our goal was to build a generalised hidden Markov model to locate genes in eukaryotic DNA using both the sequence content and evidence from genomic tiling arrays. We showed that the incorporation of tiling array data was able to improve the performance of the gene predictor, to a degree that made the resulting predictor competitive with then state-of-the-art predictors.